If two variables show a direct variation, it means that y increases/decreases each time x increases/decreases, this means that, if x increases, so do y, and if x decreases, y decreases as well.
You can express it as:
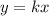
Where "k" represents the constant fo variation
If two variables have an inverse relationship, as x increases, y decreases, and vice versa.
You can express this relationship as follows:

For table "a" the values of y decrease as the values of x increase, to determine if they vary proportionally, you have to determine the value of k for each ordered pair:
To determine the constant of proportionally you have to multiply both coordinates:
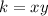
1) (-3,16)
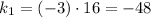
2) (4,-12)
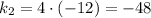
3) (6,-8)
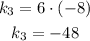
The constant of proportionality is equal for all sets of values, so you can say the relationship is proportionally inverse following the equation:
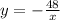
For table "b", If you compare the first two sets of values, it seems that y decreases as x increases. But If you compare the second and third ordered pairs, x increases and y is constant.
Since y does not vary for x=4 and x=6, then you can conclude that the relationship does not show a direct or indirect relationship.