Question

Consider the diagram shown below. Suppose that O=(0,0) and A=(3.6,0) and B=(3.05,1.91). The arc between points B and C is 13.824 units long.What is the value of θ1, the radian measure of ∠AOB?θ1=What is the value of θ2, the radian measure of ∠BOC?θ2=What are the x and y coordinates of point C?x=y=

Answer 1

To find the measure of an angle knowing the coordinates of the endpoint (x,y) you use the next:

`b-y_0=r\sin \theta`

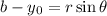
Solve the equation to θ

`\begin{gathered} (b-y_0)/(r)=\sin \theta \\ \\ \sin ^(-1)((b-y_0)/(r))=\theta \end{gathered}`

b is the coordinate in y of endpoint

y0 is the coordinate in y where is the center of the angle

r is the radius of the circle

-------------------------------------------

In this case for θ1: Endpoint B (3.05, 1.91)

b= 1.91

y0= 0 (angle in in (0,0)

r= 3.6 (The distance from the origin to point A in x is equal to the radius)

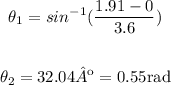
`\begin{gathered} \theta_1=sin^(-1)((1.91-0)/(3.6)) \\ \\ \theta_2=32.04º=0.55\text{rad} \end{gathered}`The radian measure of ∠AOB is 0.55. θ1 =0.55rad

-----------------------------

As you know the length of the arc BC (13.824 units long) you use the next equation to find the measure of the angle)

`S=r\cdot\theta`

Solve the equation for θ:

`\theta=(S)/(r)`

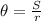
S is the length of the arc

r is the radius

In this case for θ2:

S= 13.824 units

r= 3.6

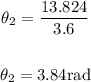
`\begin{gathered} \theta_2=(13.824)/(3.6) \\ \\ \theta_2=3.84\text{rad} \end{gathered}`The radian measure of ∠BOC is 3.84. θ2=3.84rad

---------------------------------

To find the coordinates of point C you add angles θ1 and θ2:

`\theta_1+\theta_2=0.55rad+3.84rad=4.39\text{rad}`

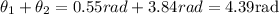
Use the next formulas to find coordinates of a endpoint with center of angle in (0,0):

`\begin{gathered} x=r\cdot\cos \theta \\ y=r\cdot\sin \theta \end{gathered}`

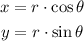
In this case for point C:

θ = 4.39rad

r= 3.6

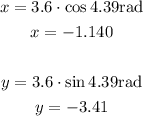
`\begin{gathered} x=3.6\cdot\cos 4.39\text{rad} \\ x=-1.140 \\ \\ y=3.6\cdot\sin 4.39\text{rad} \\ y=-3.41 \end{gathered}`The coordinates of point C are (-1.140 , -3.41)x= -1.140y= -3.41