To find the measure of an angle knowing the coordinates of the endpoint (x,y) you use the next:
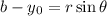
Solve the equation to θ
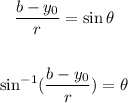
b is the coordinate in y of endpoint
y0 is the coordinate in y where is the center of the angle
r is the radius of the circle
-------------------------------------------
In this case for θ1: Endpoint B (3.05, 1.91)
b= 1.91
y0= 0 (angle in in (0,0)
r= 3.6 (The distance from the origin to point A in x is equal to the radius)
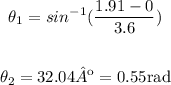
The radian measure of ∠AOB is 0.55. θ1 =0.55rad
-----------------------------
As you know the length of the arc BC (13.824 units long) you use the next equation to find the measure of the angle)
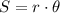
Solve the equation for θ:
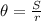
S is the length of the arc
r is the radius
In this case for θ2:
S= 13.824 units
r= 3.6
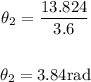
The radian measure of ∠BOC is 3.84. θ2=3.84rad
---------------------------------
To find the coordinates of point C you add angles θ1 and θ2:
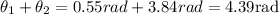
Use the next formulas to find coordinates of a endpoint with center of angle in (0,0):
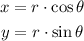
In this case for point C:
θ = 4.39rad
r= 3.6
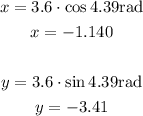
The coordinates of point C are (-1.140 , -3.41)x= -1.140y= -3.41