Since the quadratic model is
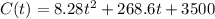
To find the equation of the tangent differentiate C(t)
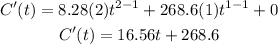
m of the tangent is equal to C'(t)
Since we need it in 2016, then substitute x by
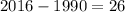
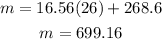
Then the equation of the tangent is
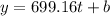
To find b substitute t by 26 in C(t) to find y, then substitute x and y in the equation of the tangent
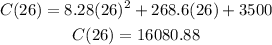
Substitute t by 26 and y by 16080.88 in the equation of the tangent to find b
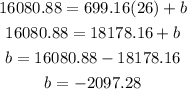
The equation of the tangent is
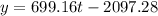

The estimated tuition in 2016 is 16080.88