Question

Need help solving thisIt’s a practice from my ACT prep guide online

Answer 1

If angles C and D are the acute angles of a right triangle, we have the image as shown below:

The question gives that:

`\sin D=(2)/(7)`

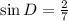
Comparing with the Sine Trigonometric Ratio given to be:

`\sin \theta=(opp)/(hyp)`

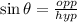
we thus have that the Sine ratio of angle D in the triangle drawn above will be:

`\sin D=(d)/(b)`

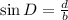
Hence, we can have the triangle look as shown below:

Therefore, the cosine of angle C, with the ratio:

`\cos C=(adj)/(hyp)`

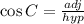
will be given to be:

`\cos C=(2)/(7)`

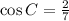
Therefore, the correct option is the FIRST OPTION.