Question

Construct a 90% confidence interval of the population proportion using the given information X =120, n= 300The lower bound isThe upper bound is

Answer 1

For this case we have the following data:

x= 120 , n= 300

The sample proportion is given by:

`p_x=(X)/(n)=(120)/(300)=(2)/(5)^{}`

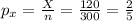
The confidence interval for a proportion is given by:

`P_x\pm z_{(\alpha)/(2)}\cdot\sqrt[]{(P_x(1-P_x))/(n)}`

The critical value for 90% confidence given is z= 1.645 and replacing we have:

`(2)/(5)\pm1.645\cdot\sqrt[]{((2)/(5)(1-(2)/(5)))/(300)}`

Then the confidence interval is:

(0.353; 0.447)