Solution
For this case we have the following data:
x= 120 , n= 300
The sample proportion is given by:
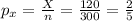
The confidence interval for a proportion is given by:
![P_x\pm z_{(\alpha)/(2)}\cdot\sqrt[]{(P_x(1-P_x))/(n)}](https://img.qammunity.org/2023/formulas/mathematics/college/92qlmn6hcee4j9o7rkuu1q981kczmpomxc.png)
The critical value for 90% confidence given is z= 1.645 and replacing we have:
![(2)/(5)\pm1.645\cdot\sqrt[]{((2)/(5)(1-(2)/(5)))/(300)}](https://img.qammunity.org/2023/formulas/mathematics/college/q9q5xikwm5t0365sq6idy9s2chx6czw8sn.png)
Then the confidence interval is:
(0.353; 0.447)