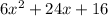Given:
Length of the prism, L = x + 2
Width of prism, W = x + 4
Height of prism, H = x
To find the surface area, use the formula already given:
Surface Area = 2LW + 2LH + 2WH
Input the values into the formula:
Surface Area = 2(x+2)(x+4) + 2(x+2)(x) + 2(x+4)(x)
Expand the parentheses:
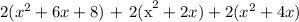
Use distributive property to multiply:
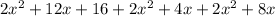
Collect like terms and evaluate:
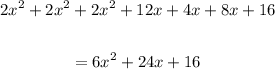
Therefore, the surface area of the rectangular prism as a polynomial in standard form is:
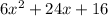
ANSWER: