Question

I need help with this practice problem solving Make sure to read the instructions on the red line

Answer 1

Given the complex number:

`2√(3)\text{ -2i}`

Step 1: Express the complex number in polar form.

In polar form, we have

`\begin{gathered} z=r(cos\theta+isin\theta)=rcis(\theta) \\ where \\ r\Rightarrow modulus\text{ of the complex number} \\ \theta\Rightarrow argument\text{ of the complex number} \end{gathered}`

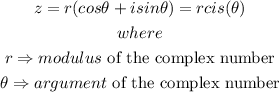
Step 2: Evaluate the modulus of the complex number,

The modulus of the complex number is expressed as

`\begin{gathered} r=√(x^2+y^2) \\ in\text{ this case,} \\ x=2√(3)\text{ ,y=-2} \\ thus, \\ r=\sqrt{(2√(3))^2+(-2)^2} \\ =√(12+4) \\ =√(16) \\ \Rightarrow r=4 \end{gathered}`

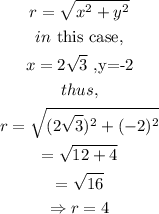
Step 3: Evaluate the argument of the complex number.

The argument of the complex number is expressed as

`\begin{gathered} \theta=\tan^(-1)((y)/(x)) \\ \Rightarrow\theta=\tan^(-1)(-(2)/(2√(3)))=\tan^(-1)(-(1)/(√(3))) \\ =-(\pi)/(6) \\ \end{gathered}`

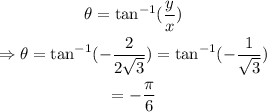
Thus, in polar form, the complex number becomes

`z=4cis(-(\pi)/(6))`

To evaluate the fourth root, we use the De Moivres's theorem.

According, to the DeMoivres's threorem,

`z^n=r^ncis(n\theta)`

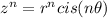
In this case,

`n=(1)/(4)`

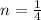
Thus,