ANSWER :
First sum : -14,625
Second sum : 11,390
EXPLANATION :
The sum formula of an arithmetic series is :

where Sn = sum
n = number of terms
a1 = first term
an = last term
From the problem, we have the series :
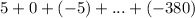
We have the first term, a1 = 5 and the last term, an = -380.
But we don't know the number of terms.
Using the nth term formula of an arithmetic series.
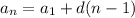
The difference in the series is 0 - 5 = -5
Let's solve for the value of n :
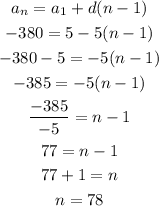
So there are 78 terms.
Now use the sum formula :
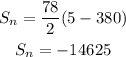
The sum is -14,625
For the second sum, we have :
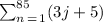
The first term will be :
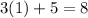
Solve for the last term at j = 85
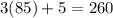
To summarized, we have :
a1 = 8
an = 260
n = 85
Using the sum formula above :
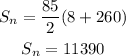
The sum is 11,390