Question

A ball is thrown upward from the top of a 160-foot-high building. The ball is 192 feet above ground level after 1 second, and it reaches ground level in 5 seconds. The height above ground is a quadratic function of the time after the ball is thrown. Write the equation of this function.

Answer 1

Let the given values represent t and f(t), where t is the x-coordinate and f(t) is the y-coordinate. Thus, the given values are points on the function:

`\begin{gathered} (t_1,f(t_1))=(0,160) \\ (t_2,f(t_2))=(1,192) \\ (t_3,f(t_3))=(5,0) \end{gathered}`

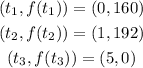
Note that f(t) represents the height of ball after t seconds.

Suubstitute the values of t and f(t) for x and y, respectively, in the quadratic equation:

`y=ax^2+bx+c`

Thus, we have the following system of equations:

Substituting (0,160) into the equation, we have:

`\begin{gathered} y=ax^2+bx+c \\ 160=a(0)^2+b(0)+c \\ 160=a(0)+b(0)+c \\ 160=0+0+c \\ 160=c \end{gathered}`

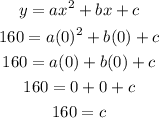
Substituting (1,192) and c = 160 into the equation, we have:

`\begin{gathered} y=ax^2+bx+c \\ 192=a(1)^2+b(1)+160 \\ 192=a(1)+b(1)+160 \\ 192=a+b+160 \\ 32=a+b \end{gathered}`

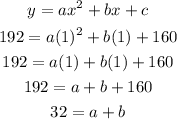
Substituting, (5,0) and c = 160 into the equation, we have:

`\begin{gathered} y=ax^2+bx+c \\ 0=a(5)^2+b(5)+160 \\ 0=a(25)+b(5)+160 \\ 0=25a+5b+160 \\ -160=25a+5b \end{gathered}`

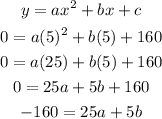
Multiply each term on both sides of the the equation 32 = a + b by -5.

`\begin{gathered} (-5)(32)=-5a-5b \\ -160=-5a-5b \end{gathered}`

Add the obtained equation to -160=25a+5b to eliminate the variable term 5b and then divide both sides by 20 to find a.

`\begin{gathered} -320=20a \\ (-320)/(20)=(20a)/(20) \\ -16=a \end{gathered}`

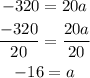
Substitute the value of a into 32 = a+b and then add both sides of the equation by 16 to find the value of b.

`\begin{gathered} 32=a+b \\ 32=-16+b \\ 48=b \end{gathered}`

Substitute the obtained values of a, b, and c into the quadratic equation.

`y=-16x^2+48x+160`

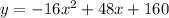
To recheck, graph the equation and determine if all of the given points are on the graph. The graph of the equation is as follows:

Note that the graph of the equation in the problem is represented on the Quadrant I only.

Since all of the points are on the equation, the quadratic equation which represents the path of the ball must be y = - 16x² + 48x + 160, where x is a non-negative number.