ANSWER
f(x) = -18x³ + 21x² + 10x - 8
Step-by-step explanation
As we can see, the x-intercepts are x = -2/3, x = 1/2 and x = 4/3. Thus, these are the zeros of the polynomial.
Given a polynomial with zeros x₁, x₂, and x₃, the polynomial's degree is 3 and it can be written with the factors,
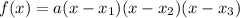
Where a is a coefficient given by the location of the y-intercept.
With the zeros, we have the function,
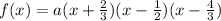
In the graph, the y-intercept is shown: (0, -8). This means that when x is 0, f(0) is -8. This is what we have to use to find the coefficient a,
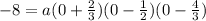
We have the product,
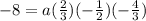
Solve the product,
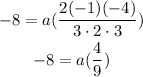
To find a, multiply both sides by 9,
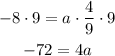
And divide both sides by 4,
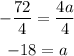
Thus the coefficient a is -18, and the function is,
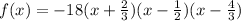
Now we have to write it in standard form. To do so, we have to multiply the factors to get a function in the form,
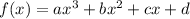
Apply the distributive property to the last two factors,
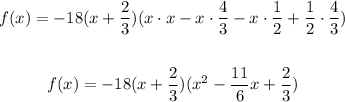
Then do the same with the first factor,
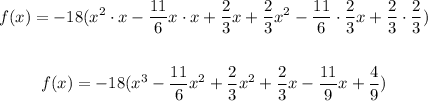
Add like terms,
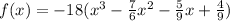
And finally, multiply each term by -18,
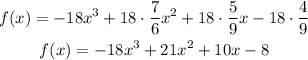
Hence, the polynomial function whose graph is in the question is f(x) = -18x³ + 21x² + 10x - 8