Question

In the diagram below, the circle has a radius of 25 inches. the area of the unshaded is 500pi in^2Determine and state the degree measure of angle Q, the central angle of the shaded sect

Answer 1

`72^(\circ)`

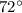
1) In this question, we are going to make use of the formula for the area of that sector, to find the central angle.

2) So, let's write it out an expression involving the area of a circle, the unshaded area, and the shaded one and then plug into that the given data:

`\begin{gathered} A=(\alpha)/(360^(\circ))*\pi r^2 \\ A_(Unshaded)+A_(shaded)=A_(Circle) \\ 500\pi+(\alpha)/(360)*\pi r^2=\pi r^2 \\ \\ 500\pi+(α)/(360)\pi25^2=25^2\pi \\ \\ 500\pi+(125\piα)/(72)=625\pi \\ \\ 500\pi +(125\pi α)/(72)-500\pi =625\pi -500\pi \\ \\ (125\pi α)/(72)=125\pi \\ \\ (72* \:125\pi α)/(72)=72* \:125\pi \\ \\ (125\pi α)/(125\pi )=(9000\pi )/(125\pi ) \\ \\ α=72^(\circ) \\ \\ \end{gathered}`

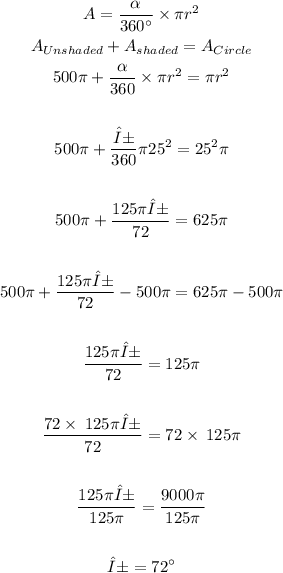
Thus, the centra angle of that shaded area is 72º