Let's call x the number of pounds of seasons choice birdseed, and y the pounds of garden mix birdseed.
The amount of pounds they wish to purchase in total is 20, then, the sum of both quantities should be 20:
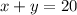
Also, they want to spend $31, so the sum of the total costs of each amount of both classes of birdseeds should add $31.
The total cost of seasons choice birdseed is 1.88 times the amount of pounds:
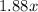
And similarly, the total cost for the amount of garden mix birdseed purchased is:
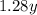
Recalling that the total cost should be $31:
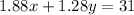
Then we have a system of two equations with two unknowns:
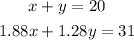
We can use the substitution method to solve it. We can begin by isolating x from the first equation:
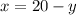
And we can now substitute the expression for x on the second equation:
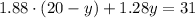
We have now a new equation where the only unknown is y. We can easily find the value of it:
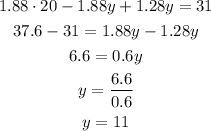
Now we know the value of y. The number of pounds of garden mix birdseed that need to be purchased is 11.
Now, from the first equation of the system, we can calculate the value of x knowing already the value of y.
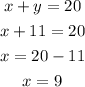
Now we know both values.
Finally, they should purchase 9 pounds of seasons choice birdseed and 11 pounds of garden mix birdseed in order to purchase 20 pounds in total and spend exactly $31.