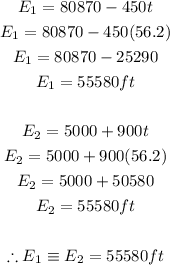Let's begin by listing out the information given to us:
8 am
airplane #1: x = 80870 ft, v = -450 ft/ min
airplane #2: x = 5000 ft, v = 900ft/min
1.
We must note that the airplanes are moving at a constant speed. The equation for the airplanes is given by:
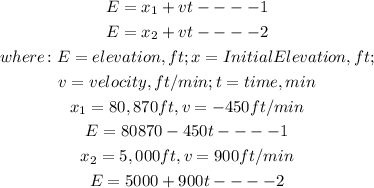
2.
We equate equations 1 & 2 to get the time both airlanes will be at the same elevation. We have:

3.
The elevation at that time (when the elevations of the two airplanes are the same) is given by substituting the value of time into equations 1 & 2. We have: