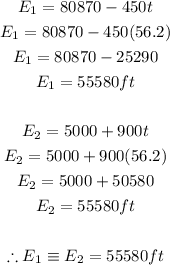Question

At 8:00 am, here's what we know about two airplanes: Airplane #1 has an elevation of 80870 ft and is decreasing at the rate of 450 ft/ min. Airplane #2 has an elevation of 5000 ft and is climbing at a rate of 900ft/min. 1) let t represent the time in minutes since 8:00 am, and let E represent the elevation in feet. Write an equation for the elevation of each plane in terms of t. 2) at what time will the two airplanes have the same elevation. 3) what is the elevation at that time?.

Answer 1

Let's begin by listing out the information given to us:

8 am

airplane #1: x = 80870 ft, v = -450 ft/ min

airplane #2: x = 5000 ft, v = 900ft/min

1.

We must note that the airplanes are moving at a constant speed. The equation for the airplanes is given by:

`\begin{gathered} E=x_1+vt----1 \\ E=x_2+vt----2 \\ where\colon E=elevation,ft;x=InitialElevation,ft; \\ v=velocity,ft\text{/}min;t=time,min \\ x_1=80,870ft,v=-450ft\text{/}min \\ E=80870-450t----1 \\ x_2=5,000ft,v=900ft\text{/}min \\ E=5000+900t----2 \end{gathered}`

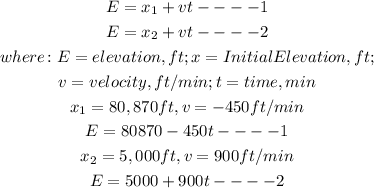
2.

We equate equations 1 & 2 to get the time both airlanes will be at the same elevation. We have:

`\begin{gathered} 5000+900t=80870-450t \\ \text{Add 450t to both sides, we have:} \\ 900t+450t+5000=80870-450t+450t \\ 1350t+5000=80870 \\ \text{Subtract 5000 from both sides, we have:} \\ 1350t+5000-5000=80870-5000 \\ 1350t=75870 \\ \text{Divide both sides by 1350, we have:} \\ (1350t)/(1350)=(75870)/(1350) \\ t=56.2min \\ \\ \text{After }56.2\text{ minutes, both airplanes will be at the same elevation} \end{gathered}`

3.

The elevation at that time (when the elevations of the two airplanes are the same) is given by substituting the value of time into equations 1 & 2. We have:

`\begin{gathered} E_1=80870-450t \\ E_1=80870-450(56.2) \\ E_1=80870-25290 \\ E_1=55580ft \\ \\ E_2=5000+900t \\ E_2=5000+900(56.2) \\ E_2=5000+50580 \\ E_2=55580ft \\ \\ \therefore E_1\equiv E_2=55580ft \end{gathered}`