Question

Jet planes can exceed the speed of sound . The mach number describes the speed of such planes. Mach 2 is twice the speed of sound. The speed of sound in air is approximately 344m/sec. complete parts a-c below:a. if the speed of a plane is described as Mach 2.5 what is it's speed in kilometers per hour? b. if the speed of a plane is described as Mach 3.8, what is it's speed in meters per second?c. Describe the speed of 3150 km/hr as a Mach number.

Answer 1

Since Mach 2 is twice the speed of sound and the speed of sound is 344 m/sec, then Mach 2 is

`2*344=688\text{ m/sec}`

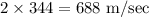
a.

If the speed of a plane is Mach 2.5, then

`(2)/(2.5)=(688)/(x)`

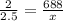
By using cross multiplication

`\begin{gathered} 2* x=2.5*688 \\ 2x=1720 \end{gathered}`

Divide both sides by 2

`x=860\text{ m/sec}`

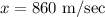
Now we need to change it to km per h

Since 1 km = 1000 m, 1 h = 60 x 60 = 3600 sec, then

`((860)/(1000))/((1)/(3600))=3096\text{ km/h}`

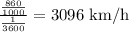
b.

Since the speed of the plane is Mach 3.8, then

`(2)/(3.8)=(688)/(y)`

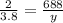
By using cross multiplication

`\begin{gathered} 2* y=3.8*688 \\ 2y=2614.4 \end{gathered}`

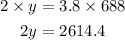
Divide both sides by 2

`\begin{gathered} (2y)/(2)=(2614.4)/(2) \\ y=1307.2\text{ m/sec} \end{gathered}`

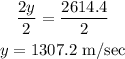
The speed is 1307.2 m/sec

c.

Since the speed is 3150, then

Change it to m/sec

`(3150*1000)/(1*60*60)=875\text{ m/sec}`

Now let us find the Mach number

`(2)/(z)=(688)/(875)`

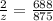
By using cross multiplication

`\begin{gathered} 688* z=2*875 \\ 688z=1750 \end{gathered}`

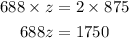
Divide both sides by 688

`\begin{gathered} (688z)/(688)=(1750)/(688) \\ z=2.5436 \end{gathered}`

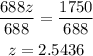
The Mach number is about 2.544