Since Mach 2 is twice the speed of sound and the speed of sound is 344 m/sec, then Mach 2 is
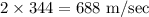
a.
If the speed of a plane is Mach 2.5, then
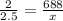
By using cross multiplication
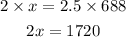
Divide both sides by 2
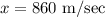
Now we need to change it to km per h
Since 1 km = 1000 m, 1 h = 60 x 60 = 3600 sec, then
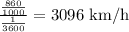
b.
Since the speed of the plane is Mach 3.8, then
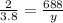
By using cross multiplication
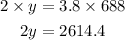
Divide both sides by 2
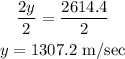
The speed is 1307.2 m/sec
c.
Since the speed is 3150, then
Change it to m/sec
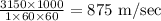
Now let us find the Mach number
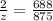
By using cross multiplication
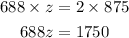
Divide both sides by 688
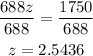
The Mach number is about 2.544