Answer:
(a)0.208
(b)0.633
Step-by-step explanation:
Since the variable X is not defined, we assume that X is the number of questions answered correctly.
Each question has 4 options out of which just 1 is correct.
Each question is independent of other questions. Thus, we can use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
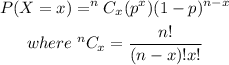
• In this case, there are 8 questions: n=8
,
• 1 out of 4 options is correct, p=1/4=0.25
Part 1
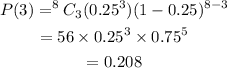
P(3)=0.208 correct to 3 decimal places.
Part 2
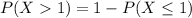
First, we calculate P(X≤1):
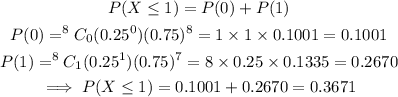
Therefore, the probability, P(more than 1) is:
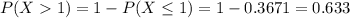
P(more than 1) is 0.633 (correct to 3 decimal places).