Question

the floor of a moving van is 3 ft off the ground the rap into the band makes a 12 degree angle with the ground how long is the ramp

Answer 1

The floor of a moving van is 3 ft off the ground.

The ramp into the van makes a 12-degree angle with the ground.

How long is the ramp?

Let us draw a figure to better understand the problem.

As you can see from the above figure,

In the above triangle, with respect to angle 12°, the opposite side is 3 ft and the hypotenuse is x

The hypotenuse (x) is the length of the ramp that we need to find.

Recall from the trigonometric ratios,

`\sin \theta=\frac{\text{opposite}}{\text{hypotenuse}}`

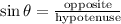
For the given case,

θ = 12°

Opposite = 3

Hypotenuse = x

Let us substitute these values into the above formula

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \sin 12\degree=(3)/(x) \\ x=(3)/(\sin 12\degree) \\ x=(3)/(0.2079) \\ x=14.43\: ft \end{gathered}`

Therefore, the ramp is 14.43 ft long.