The following were the observed points of the triangles as shown in the image provided:
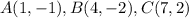

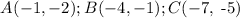
The transformation of triangle ABC to A'B'C' is of the rule (x, y) to (-x, -y). This rule represents a 180-degree counterclockwise rotation
The transformation of triangle A'B'C' to A"B"C" is of the rule (x, y) to (x, y-3). This rule represents a translation down by 3 units
Hence, ABC is rotated 180 degrees counterclockwise about the origin to become A'B'C'. Then A'B'C' is translated 3 units down to become A"B"C" the transformation are both rigid, the pre-image and image are congruent