Let e be the speed of the eastbound train, and w be the speed of the westbound train. Since the eastbound train travels 14 miles per hour faster than the westbound train, we'll have that
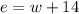
If after 2 hours the trains are 272 miles apart, we can say that:
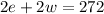
Thereby, we'll have the following system of equations:
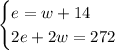
Since we already have e in terms of w, let's go ahead and plug it in the second equation, and solve for w :
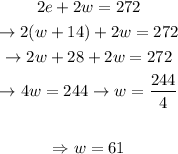
Now we've found w, let's plug in its value in equation 1 to find e :
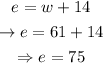
Therefore, we can conclude that the eastbound train is traveling at 75 mph, and the westbound train is traveling at 61 mph