Let us start by illustrating the problem using a diagram:
To find the measure of angle A, we need to first find the length of the side opposite angle C using cosine rule:
Cosine rule is defined to be:
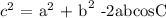
Substituting the given sides and angle:
Let c be the side opposite angle C, b be the side opposite angle B and a be the side opposite angle A
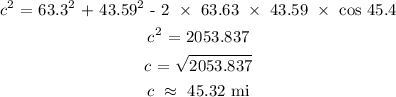
Hence, we have the triangle:
The next step is to use sine rule to find the measure of angle A
Sine rule is defined as:
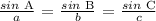
Applying sine rule:
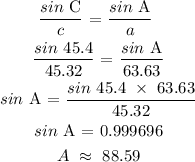
Answer:
Measure of angle A = 88.59 degrees