Question

Find the measure of angle ASolve the right triangle. a=63.63 mi, b= 43.59 mi, C= 45.4 degrees

Answer 1

Let us start by illustrating the problem using a diagram:

To find the measure of angle A, we need to first find the length of the side opposite angle C using cosine rule:

Cosine rule is defined to be:

`c^2\text{ = a}^2\text{ + b}^2\text{ -2abcosC}`

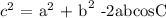
Substituting the given sides and angle:

Let c be the side opposite angle C, b be the side opposite angle B and a be the side opposite angle A

`\begin{gathered} c^2\text{ = 63.3}^2\text{ + 43.59}^2\text{ - 2 }*\text{ 63.63 }*\text{ 43.59 }*\text{ cos 45.4} \\ c^2\text{ = 2053.837} \\ c\text{ = }√(2053.837) \\ c\text{ }\approx\text{ 45.32 mi} \end{gathered}`

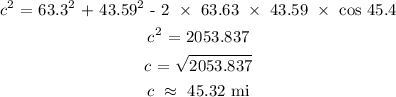
Hence, we have the triangle:

The next step is to use sine rule to find the measure of angle A

Sine rule is defined as:

`\frac{sin\text{ A}}{a}\text{ = }\frac{sin\text{ B}}{b}\text{ = }\frac{sin\text{ C}}{c}`

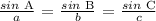
Applying sine rule:

`\begin{gathered} \frac{sin\text{ C}}{c}\text{ = }\frac{sin\text{ A}}{a}\text{ } \\ \frac{sin\text{ 45.4}}{45.32}\text{ = }\frac{sin\text{ A}}{63.63} \\ sin\text{ A = }\frac{sin\text{ 45.4 }*\text{ 63.63}}{45.32} \\ sin\text{ A = 0.999696} \\ A\text{ }\approx\text{ 88.59} \end{gathered}`

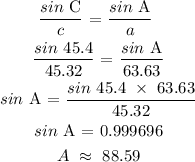
Answer:

Measure of angle A = 88.59 degrees