Answer:

Explanation:
The angle between two vectors is represented by the following equation:
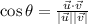
Notice that it involves a trigonometric function, the dot product of two vectors, and the magnitude of two vectors.
Then, let's determine the dot product of the two vectors:
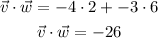
Now, calculate the magnitudes of the vectors:
![\begin{gathered} \lvert\vec{v}\rvert=\sqrt[]{(-4)^2+(-3)^2}=5 \\ \lvert\vec{w}\rvert=\sqrt[]{(2)^2+(6)^2}=2\sqrt[]{10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4irxub2ilala1mrheoi78amzbptwywsv0r.png)
Now, substitute into the equation to find the angle:
![\begin{gathered} \cos \theta=\frac{-26}{5\cdot2\sqrt[]{10}} \\ \theta=\cos ^(-1)(\frac{-26}{5\cdot2\sqrt[]{10}}) \\ \theta=\text{ 145.3\degree} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jboe55zdk3juaus6crmjv9nsnant6ru628.png)