Question

Solve for x with solution
`(9x-7)/(3x+5) =(3x-4)/(x+6)`

Answer 1

Answer: " x= \frac{18}{41} " ; {x\\eq \frac{-5}{3} ; 6}.

Explanation:

To solve: We cross-factor multiply:
that is:
"
`(a)/(b) =(c)/(d)` " ;
`ad = bc` ; {
`{b\\eq 0` ,
`d\\eq 0`}.

___
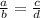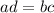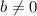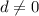So: both of the denominators cannot equal 0; since one cannot "divide by zero" ;

So,
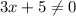`3x+5 \\eq 0` ; and:
`x + 6 \\eq 0` ;

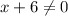So: Consider:
3x + 5 = 0 ; Solve for x (one of the values that x cannot equal):

Subtract each side of the equation by 5 ;

3x + 5 − 5 = 0 − 5 ;

to get: 3x = -5 ;

Now: Divide each side of the equation by 3; to isolate x

on one side of the equation; & to solve for x :

3x / 3 = -5 /3 ; to get: x= -5/3 ; so: "
`x\\eq (-5)/(3)` " ;
___
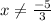Then: Consider: x + 6 = 0 ;
Solve for x (one of the values that x cannot equal):
Subtract each side of the equation by 6; to isolate x on one side of the equation; & to solve for x :
x + 6 − 6 = 0 − 6 ;

to get "x = -6 " ; so: "
`x\\eq -6` " .
___
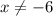Now: Cross-factor multiply:
(9x − 7)(x + 6) = (3x + 6)(3x − 4) ;

___
Note the following:
(a + b)(c + d) = ac + ad + bc + bd ;
___
Let us start with the 'left-hand' side of the equation:
(9x*x) + (9x*6) + (-7*x) + (-7*6) ;
9x² + 55x + (-7x) + (-42) ;
→ 9x² + 55x − 7x − 42 ;

Combine the "like terms":
+ 55x − 7x = + 48x ;

Rewrite: → 9x² + 48x − 42 ;
___
Then: Let's continue with the 'right-hand' side of the equation:
(3x + 6)(3x − 4) ;

(3x*3x) + (3x*-4) + (6*3x) + (6*-4) ;

9x² + (-12x) + (18x) + (-24) ;

→ 9x² − 12x + 19x − 24 ;

Combine the "like terms" :
-12x + 19x = + 7x ;

Rewrite:
→ 9x² + 7x − 24 ;
Now, rewrite the entire equation:
9x² + 48x − 42 = 9x² + 7x − 24 ; and simplify:

-9x² − 7x + 24 = - 9x² − 7x + 24 ;

41x − 18 = 0 ;

Now, add 18 to each side of the equation:
41x − 18 + 18 = 0 + 18 ;

to get: 41x = 18 ;

Now, divide each side of the equation by 41; to isolate x on one side of the equation; & to solve for x :
41x / 41 = 18/ 41 ;

"
`x= (18)/(41)` " ; {
`x\\eq (-5)/(3)` ;
`6` } .
___
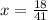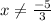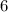Hope this helps! Best wishes!
___