Answer:
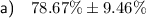
or d) None of the answers are correct. (Please see notes below).
Step-by-step explanation:
P-hat is the probability that a given outcome will occur given a specified sample size.

Given:
Substitute the given values into the formula to find p-hat:
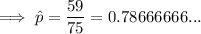
The critical value for a 95% confidence level using normal distribution is:


Substitute the given values into the margin of error formula:
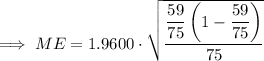
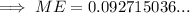
Therefore, an estimate of the proportion of young-adult novels that include a love triangle (including a margin of error) is:
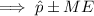
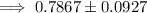
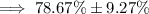
This result if not given in the list of answer options. However, the final result depends on the accuracy of the z-score and p-hat used in the calculations.
If we round the critical value to the nearest integer then:
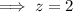
Substitute the rounded z-value into the margin of error formula:
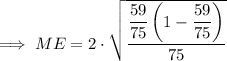
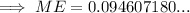
Therefore, an estimate of the proportion of young-adult novels that include a love triangle (including a margin of error) using z = 2 is:
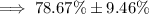
Note: It is likely that this question required the critical value to be rounded to the nearest integer, however please note that this is not normal practice as it produces a different result, as evidenced above.