Question

A university wants to determine the average salary of its graduating computer science majors. The university asks the graduating classes of 50 students to share their starting salaries when hired. The 50 students had an average salary of $100,000 with a standard deviation of $2,000. Find a 95% confidence interval for the average starting salary of computer science majors from the university.A) ($99,431.61, $100.568.39)B) ($99,445.64, $100,554.36)C) ($99,982.26, $100,017.74)D) The salaries are not normally distributed so we cannot compute a confidence interval

Answer 1

For this problem we use the following formula for the confidence interval:

`CI=x_m\pm z\frac{s}{\sqrt[]{n}}`

CI confidence interval

xm is the sample mean

z confidence level value

s sample standard deviation

n sample size

Now, we input the given data:

xm= 100000

z= 1.960

s=2000

n=50

`\begin{gathered} CI_(\max )=100,554.36 \\ CI_(\min )=99,445.64 \end{gathered}`

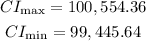
Solution is option B)