1 Answer

Mohammad Misbah · Answer 1 · 2023-06-15T07:11:01+0000

Hello there. To solve this question, we'll have to perform long division to find the quotient of the division of the following polynomials:

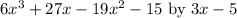
$6x^3+27x-19x^2-15\text{ by }3x-5$

We use the following algorithm to divide the polynomials

Above the line, we put the terms that, when multiplied by the terms of (3x - 5), will give us a term from the cubic polynomial.

Start multiplying it by 2x², since 2x² * 3x = 6x³; then subtract it from the polynomial:

Don't forget to multiply the remaining terms

Now, multiply it by -3x, because (-3x) * 3x = -9x². Subtract it from the polynomial:

Finally, multiply it by 4, becuase 4 * 3x = 12x.

Notice that now we can no longer divide the polynomial because its degree is less than the degree of the divisor.

So we say that

$\boxed{\begin{equation*} 6x^3+27x-19x^2-15=(3x-5)\cdot(2x^2-3x+4)+5 \end{equation*}}$

Another way of getting this same result is to use the Horner-Ruffini device:

Please log in or register to add a comment.