Given,
The table of scale factor, ratio of area and ratio of volume is,
Required:
The ratio of area and volume of the similar solids.
The scale factor is 2:3.
The ratio in area is:
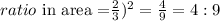
The ratio in volume is:
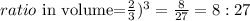
The ratio of the area is 50:72.
The scale factor of the solid is:
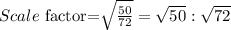
The ratio in volume is:
![Scale\text{ factor=\lparen}\sqrt{(50)/(72)})^3=\sqrt[3]{50}:\sqrt[3]{72}](https://img.qammunity.org/2023/formulas/mathematics/college/su4g3xdiaqjbun1dgwg5ok739yxspkcwk6.png)
The ratio in the volume is 27:64.
The scale factor of the solid is:
![Scale\text{ factor=}\sqrt[3]{(27)/(64)}=3:4](https://img.qammunity.org/2023/formulas/mathematics/college/w2szmk0c4cw8v5bhv04ycf9kudgz033bf2.png)
The ratio in the area is,
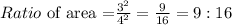
Hence, the ratio of area and volume of the solids is obtained.