We are given the following information of a projectile motion.
Initial horizontal velocity of ball = 8.2 m/s
Distance covered by ball = 41 m
1. The time required for the ball to reach the ground.
The time can be found as
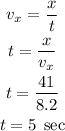
Therefore, the time required for the ball to reach the ground is 5 seconds.
2. The height of the window of the building from which the ball was thrown.
The vertical height can be found as

Where voy is the initial vertical component of the velocity that is 0, g is the acceleration due to gravity, y0 is the height of the window building that we need to find, and yf is the height of the ball when the ball hits the ground that is 0.
Let us substitute the given values and solve for y0
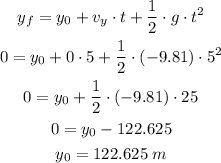
Therefore, the height of the window of the building from which the ball was thrown is 122.625 m
3. The vertical component of the ball's velocity at the moment it hits the ground.
The vertical component of the ball's velocity can be found as
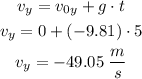
Therefore, the vertical component of the ball's velocity at the moment it hits the ground is 49.05 m/s
The negative sign indicates that the direction of the velocity is downward which makes sense.