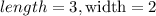Question

Find the maximum area of a rectangle and the dimensions of the rectangle question

Answer 1

Given the question in the image, the following are the solution steps to answer the question

STEP 1: Write the given sides

`\begin{gathered} \text{length}=3x \\ \text{width}=(4-2x_{}) \end{gathered}`

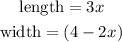
STEP 2: Calculate the area

`\begin{gathered} \text{Area}=\text{length}* width \\ \text{Area}=3x*(4-2x) \\ \text{Area}=3x(4)+3x(-2x) \\ \text{Area}=12x-6x^2 \end{gathered}`

STEP 3: Calculate the maximum area of the rectangle

Set the differential to zero to get x

`\frac{d^{}(\text{area)}_{}}{d(x)}=0`

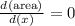
STEP 4: Find the first differential of the derived Area in step 2

`\begin{gathered} \text{Area}=12x-6x^2 \\ \frac{d(\text{area)}}{dx}=12-12x \end{gathered}`

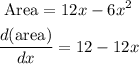
STEP 5: Set the differential to zero to get x

`\begin{gathered} 12-12x=0 \\ 12=0+12x \\ 12=12x \\ \text{Divide both sides by 12} \\ (12)/(12)=(12x)/(12) \\ x=1 \end{gathered}`

STEP 6: Substitute 1 for x in the area formula in Step 2

`\begin{gathered} \text{Area}=12x-6x^2 \\ x=1 \\ \text{Area}=12(1)-6(1^2) \\ \text{Area}=12-6=6 \end{gathered}`

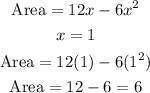
Hence, the maximum area of the reactangle is 6

STEP 7: Get the vertex

Using the formula for area in step 2

`\begin{gathered} Area=-6x^2+12x \\ \text{comparing with general quadratic form, a=-6,b=12} \\ \Rightarrow x\text{ vertex=}-(b)/(2a)=-(12)/(2(-6))=-(12)/(-12)=1 \\ \Rightarrow(1,6) \\ substitute\text{ 1 for x to get y vertex} \\ -6(1^2)+12(1)=-6+12=6 \\ y\text{ vertex=6} \\ \text{vertex}=(1,6) \end{gathered}`

Hence, the vertex is (1,6)

STEP 8: Find the dimensions of the rectangle

`\begin{gathered} \text{length}=3x \\ x=1 \\ \text{length}=3(1)=3 \\ \text{width}=4-2x \\ x=1 \\ \text{width}=4-2(1)=4-2=2 \end{gathered}`

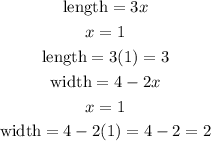
Hence, the dimensions of the rectangle are:

`length=3,\text{width}=2`