Given:
The coordinates of points is
(x1, y1)=(4, 2)
(x2, y2)=(2, -5).
The slope of the line passing through points (x1, y1)=(4, 2) and (x2, y2)=(2, -5) is,
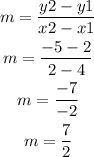
The point slope form of the equation of a line can be written as,
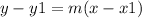
Put (x1, y1)=(4, 2) in the above equation to find the equation of a line with slope m=7/2 and passing through (4,2).
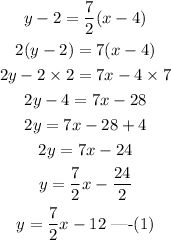
The general equation of a straight line is,
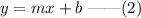
Here, m is the slope of the line and b is the y intercept.
Comaparing equations (1) and (2), we get y intercept b=-12.
Therefore, the y intercept b=-12.
The equation of the line is,

We have to check if (-4, -2) is a point on the line.
For that put x=-4 in equation (3) and solve for y to check if we get y=-2.
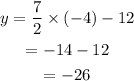
Since we got y=-26 instead of , (-4, -2) is not a point on the line.