Question

Does the series 2+1+¹+1+...2+1 =+ = + 328converge, or diverge? If it converges, what is the sum

Answer 1

Answer:

The sum of the geometric series = 11.93

Step-by-step explanation:

The sum of the first n terms of a geometric series is:

`S_n=(a(1-r^n))/(1-r)`

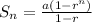
From the given expression:

The first term, a = 3

The common ratio, r = 3/4 = 0.75

The number of terms, n = 18

Substitute the given values into the formula above

`\begin{gathered} S_(18)=(3(1-0.75^(18)))/(1-0.75) \\ \\ S_(18)=(3(1-0.00563771011))/(0.25) \\ \\ S_(18)=(2.98308686966)/(0.25) \\ \\ S_(18)=11.93 \\ \end{gathered}`

The sum of the geometric series = 11.93