Question

The side of a parallelogram has endpoints at (2, 1) and (3, 5). The endpoints for the opposite side are (5, 2) and (6, 6).What are the lengths and slopes of the pairs of opposite sides?

Answer 1

Let's start making a drawing of the situation of the question

We have to calculate the length and the slope of the sides in red

length:

To find the length, we can find the distance between the points, so we can use the formula

`d=√((x_1-x_2)^2+(y_1-y_2)^2)`

where d is the distance between the points

`(x_{1\text{ }},y_{1\text{ }})\text{ and \lparen x}_2,y_(_2))`

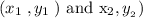
In our case, we have to calculate two distances, the first one is between the points

`(2,1)\text{ and \lparen3,5\rparen}`

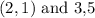
Putting this coordinates into the formula for the distance, we get:

`d=√((2-3)^2+(1-5)^2)=√((-1)^2+(-4)^2)=√(1+16)=√(17)`

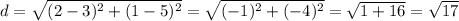
The length of the other side, is not necessary, the reason for that , is that since opposite sides in a parallelogram have the same length we conclude the opposite side have length

`√(17)`

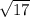
Finally let's calculate the slope, we can use the formula to the slope between two points

`m=\frac{y_{2\text{ }}-y_{1\text{ }}}{x_2-x_1}`

Again, we will calculate the slope for the of the segment between the points

`(2,1)\text{ and \lparen3,5\rparen}`

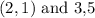
applying the formula, we arrive in

`m=(5-1)/(3-2)=(4)/(1)=4`

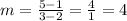
so the slope is m=4. Again as we are in a parallelogram the opposite side have to have the same slope.

Looking at the option for this question, we conclude: The option a) is the correct answer.