In order to calculate the height separating the bottom 90% from the top 10%, first let's find the equivalent z-score for a probability of 90% in the z-table.
Looking at the z-table, the z-score for a probability of 90% is equal to approximately 1.28.
Then, to calculate the height, let's use the formula below for the z-score:
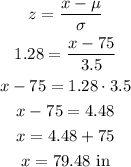
So the wanted height is equal to 79.48 inches.