Question

Mr. Mangan launches himself from a cannon with an initial velocity of100 m/s at an angle of 45 degrees above the ground. How high doeshe go and how far does he go?

Answer 1

First, we need to calculate the horizontal and vertical components of the velocity:

`\begin{gathered} Vx=V\cdot\cos (\theta) \\ Vx=100\cdot\cos (45\degree) \\ Vx=100\cdot0.707=70.7\text{ m/s} \\ \\ Vy=V\cdot\sin (\theta) \\ Vy=100\cdot\sin (45\degree) \\ Vy=100\cdot0.707=70.7\text{ m/s} \end{gathered}`

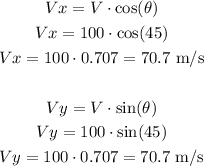
Now, to find the maximum height, at this point the velocity is zero, so let's use Torricelli's equation, with the acceleration being the gravity (9.8 m/s2):

`\begin{gathered} V^2=V^2_0+2\cdot a\cdot d \\ 0=70.7^2-2\cdot9.8\cdot d \\ 19.6d=4998.49 \\ d=255.02\text{ m} \end{gathered}`

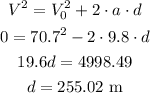
So the maximum height is 255.02 meters.

Now, to find how far does he go, let's find the amount of time he is in the air, calculating the rising time and multiplying by 2:

`\begin{gathered} V=V_0+a\cdot t \\ 0=70.7-9.8t \\ 9.8t=70.7 \\ t=7.21\text{ s} \\ \\ 2t=2\cdot7.21=14.42\text{ s} \end{gathered}`

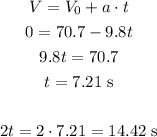
Using this time for the horizontal movement, we have:

`\begin{gathered} d=v\cdot t \\ d=70.7\cdot14.42 \\ d=1019.49\text{ m} \end{gathered}`

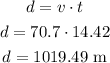
So the horizontal distance traveled is 1019.49 m.