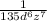The expression to simplify is:
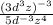
First, we will use the power rule of exponents to simplify the numerator. The rule is:
Simplifying, we have:
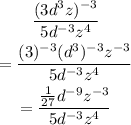
Now, we use another exponent rule shown below to simplify it further. The rule is:
So, we have:
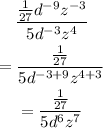
Now, we can just simplify the constants to get our final answer:
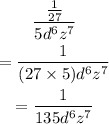
The final answer is: