Question

The path of debris from a firework display on a windy evening can be modeled by the equation y = -0.04x2 + 2x + 8, where y is the height and x is the horizontal distance in feet. Do not round your answers.1. How far away from the launch site will the debris land? 2. How high will the fireworks reach?

Answer 1

You have the following function for the height of debris:

`y=-0.04x^2+2x+8`

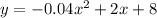
In order to answer the given questions, consider that the graph of the given function is:

1) The distance at which the debris land is given by one of the zeros of the function, because y is a parabolla, as you can notice in the previous image.

Use the quadratic formula to find the zeros of the function:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

coefficients a, b and c are the coefficients of the quadratic function ax^2+bx+c. In this case, by comparing with the given expression for y, you have:

a = -0.04

b = 2

c = 8

Replace the previous values into the quadratic formula and simplify:

`\begin{gathered} x=\frac{-2\pm\sqrt[]{(2)^2-4(-0.04)(8)}}{2(-0.04)} \\ x=\frac{-2\pm\sqrt[]{4+1.28}}{-0.08} \\ x=\frac{-2\pm\sqrt[]{5.28}}{-0.08} \\ x=(-2\pm2.297825059)/(-0.08) \end{gathered}`

select only the positive result because it has physical meaning:

`x=(-2-2.297825059)/(-0.08)=53.72281323`

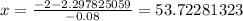
Hence, the debris are at a distance of 53.72281323 feet from the launching site.

2) The maximum height reached by fireworks, is represented by the y-coordinate of the vertex point of the parabolla (as you can notice in the graph).

The x-coordinate of the vertex of a parabolla is given by:

`x=-(b)/(2a)`

Replace the values of a and b, and simplify:

`x-=-(2)/(2(-0.04))=25`

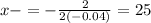
The value of y for the previous value of x is:

`\begin{gathered} y=-0.04(25)^2+2(25)+8 \\ y=-0.04(625)+50+8 \\ y=-25+50+8 \\ y=33 \end{gathered}`

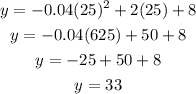
The previous value is the y-coordinate of the vertex.

Hence, the maximum height reached by the fireworks is 33 feet