From the table,
The total number of persons, n(s)=14,502.
a)
To find the probability that the selected person does not have a Ph.D.
The number of persons does not have a Ph.D is,
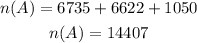
So, the probability is,
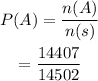
Hence, the answer is,

b) To find the probability that the selected person does not have a Master's degree
The number of person does not have a Master's degree is,
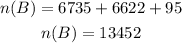
So, the probability is,
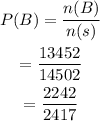
Hence, the answer is,
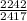
c)
To find the probability that the selected person is female or has a Master's degree
Let n(C) be the number of females.
Let n(D) be the number of persons have master's degree.
Let n(CnD) be the number of persons who both female and have master's degree.
Using the formula,

So,