We will determine the times the volume of the cylinder is bigger as follows:
*First: We determine the volume of the pipe:
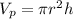
*Second: We determine the volume of the holding tank:
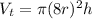
*Third: Since the length(h) will be the same for both cylinders, we will assing an arbitrary value for it [When we assign this value no matter what number it might be, except of course 0, the result will be the same]. In our case, to make it "easier" or more intuitive we will work with h = 1, so, we would have:
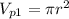
&
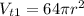
*Fourth: We determine the scale factor:
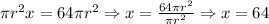
So, the volume of the holding tank is 64 times greater than the volume of the tube. [Option 4]