Answer:
Concept:
To figure out the equation of the graph, we will use the image below and bring out the two intercepts
The two intercepts from the graph are
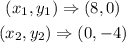
To figure out the equation of the line, we will use the formula below
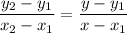
By substituting the values, we will have
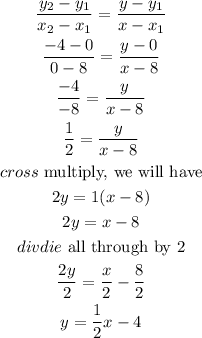
Graphically, we will have
Hence,
The final answer is
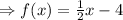
OPTION A is the right answer