The fifth and tenth terms of an arithmetic sequence respectively are - 2 and 53 what is the seventh term of the sequence?
Answer :
Step 1:
Using the nth term of an Arithmetic Progression,
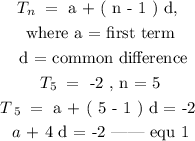
On the other hand,
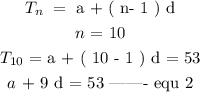
Step 2 :
We need to solve the two sets of linear equations, we have that:
![undefined]()