Question

Consider the equation 7 • e^0.1t = 47.Solve the equation for t. Express the solution as a logarithm in base-e.t = ___Approximate the value of t . Round your answer to the nearest thousandth.t ≈ ___

Answer 1

The solution of the equation expressing it as a logarithm in base-e is t = ln (6.714)/0.1.

The approximate value of t = 19.042.

How to calculate the value of t?

The solution of the equation expressing it as a logarithm in base-e is calculated as follows;

The given equation;

`7 * e^(0.1t) = 47`

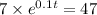
We will divide both sides of the equation by 7;

`(7 * e^(0.1t) )/(7) = (47)/(7)`

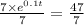
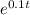`e^(0.1t)` = 6.714

Take log of both sides of the equation;

`\log (e^(0.1t)) = \log (6.714)`

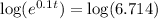
0.1t (ln e) = ln (6.714)

t = ln (6.714)/0.1

The approximate value of t is calculated as;

t = ln (6.714)/0.1

t =1.9042 / 0.1

t = 19.042

t ≈ 19.042

Answer 2

Answer:
`\begin{gathered} t=10\log_e47 \\ \\ \approx38.501 \end{gathered}`

Step-by-step explanation:

Given the equation:

`e^(0.1t)=47`

Applying logarithm to both sides:

`\begin{gathered} \log_ee^(0.1t)=\log_e47 \\ \\ 0.1t\log_ee=\log_e47 \\ \\ 0.1t=\log_e47 \\ \\ t=(1)/(0.1)\log_e47 \\ \\ t=10\log_e47 \end{gathered}`

Aproximately, we have:

`t=38.501`