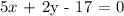The equation is given as,
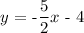
Converting the given equation to standard form,
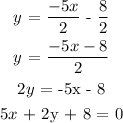
The slope of the given line is calculated as,
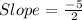
As the required line is parallel to the given line. Therefore slope of the required line is equal to the given line which is -5/2.
The required line passes through the point (5, -4).
The equation of a required line is calculated using the slope point formula.
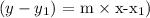
Where,
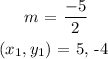
Required equation is calculated as,
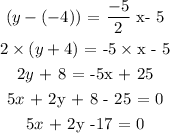
Thus the equation of the required line is,