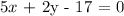Question

points possible197 24 answeredQuestion 23Write the equation of a line parallel to the line:5y = - 22-4that goes through the point (5, 4).Write your equation in slope intercept form, using reduced fractions for the slope and intercept ifnecessary> Next Question

Answer 1

The equation is given as,

`\begin{gathered} y\text{ = -}(5)/(2)x\text{ - 4} \\ \\ \\ \end{gathered}`

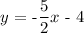
Converting the given equation to standard form,

`\begin{gathered} y\text{ = }(-5x)/(2)\text{ - }(8)/(2) \\ y\text{ = }(-5x-8)/(2) \\ 2y\text{ = -5x - 8} \\ 5x\text{ + 2y + 8 = 0} \end{gathered}`

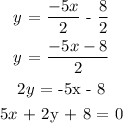
The slope of the given line is calculated as,

`Slope\text{ = }(-5)/(2)`

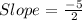
As the required line is parallel to the given line. Therefore slope of the required line is equal to the given line which is -5/2.

The required line passes through the point (5, -4).

The equation of a required line is calculated using the slope point formula.

`(y-y_1)\text{ = m}*\text{\lparen x-x}_1)`

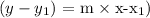
Where,

`\begin{gathered} m\text{ = }(-5)/(2) \\ (x_1,y_1)\text{ = \lparen 5, -4 \rparen} \end{gathered}`

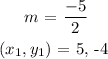
Required equation is calculated as,

`\begin{gathered} (y-(-4))\text{ = }(-5)/(2)\text{ \lparen x- 5\rparen} \\ 2*(y+4)\text{ = -5}*\text{\lparen x - 5\rparen} \\ 2y\text{ + 8 = -5x + 25} \\ 5x\text{ + 2y + 8 - 25 = 0} \\ 5x\text{ + 2y -17 = 0} \end{gathered}`

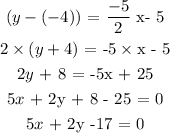
Thus the equation of the required line is,

`5x\text{ + 2y - 17 = 0}`