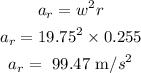Question

A 51 cm diameter wheel accelerates uniformly about its center from 150 rpm to 290 rpm in 4.0 s. (A)Determine the radial component of the linear acceleration of a point on the edge of the wheel 1.1 s after it has started accelerating.

Answer 1

Answer:

Radial component of the linear acceleration = 99.47 m/s^2

Explanations:

The diameter of the wheel, d = 51 cm

The radius, r = d/2 = 51/2 = 25.5 cm

r = 25.5/100 = 0.255 m

r = 0.255 m

`\begin{gathered} N_{i\text{ }}=\text{ 150 rpm} \\ w_i=\text{ 150}*(2\pi)/(60) \\ w_i=\text{ }15.71\text{ rad/s} \end{gathered}`
`\begin{gathered} N_f=\text{ 290 rpm} \\ w_f=\text{ 290}*(2\pi)/(60) \\ w_f=\text{ }30.37\text{ rad/s} \end{gathered}`
`\begin{gathered} w_f=w_i+\alpha t \\ 30.37=15.71+4\alpha \\ 4\alpha=30.37-15.71 \\ 4\alpha=\text{ }14.66 \\ \alpha=(14.66)/(4) \\ \alpha\text{ = }3.67rad/s^2 \end{gathered}`

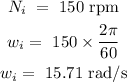
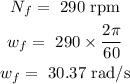
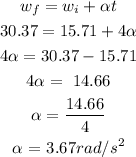
At t = 1.1, first calculate the new angular velocity

`\begin{gathered} w=w_1+\alpha t \\ w\text{ = 15.71+3.67(1.1)} \\ w\text{ = 15.71+}4.04 \\ w\text{ = }19.75\text{ rad/s} \end{gathered}`

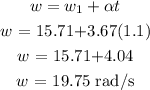
The radial component of the linear acceleration is given as:

`\begin{gathered} a_r=w^2r \\ a_r=19.75^2*0.255 \\ a_r=\text{ }99.47\text{ m/}s^2 \end{gathered}`