Question

Can someone help me with this? Is the answer B?

Answer 1

The quadratic function, with a > 0, have an interesting property, it's always negative in the interval between the zeros, we can see it graphically:

But why it's important? When we are doing an inequation with quadratics, we always solve the quadratic first. Looking at the picture we can see that the only part not shaded is the interval (1,-1). It's a hint for us.

Let's analyze each equation.

A)

`x^2>-1`

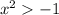
When a number squared is bigger than -1? always, then it's not the correct answer.

B)

`x^2\le1`

We can rewrite that equation as

`x^2-1\le0`

When the quadratic x^2 - 1 is equal to or less than 0 (negative)? between its zeros, the zeros are 1 and -1, therefore if cannot be our answer because it's inverted, a graph of the inequality would be the interval [1, -1]

C)

It's the same thing as B, but not zero is not included, again, cannot be our answer;

D)

Now we have

`\begin{gathered} x^2>1 \\ \\ x^2-1>0 \end{gathered}`

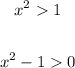
We have the same inequation, but now we want to graph when the function is bigger than 0. We saw that it's zero at 1 and -1, and between 1 and -1 it's negative! then the graph of the inequation matches the graph of the picture! That's our answer

The correct answer is the letter D. x² > 1

You can see it better at the graph