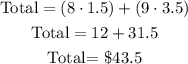Question

Customer 1 buys 2 hamburgers and 4 drinks, and his total is $13.00. Customer 2 buys 3 hamburgers and 7 drinks, and his total comes out as $21.00. PART A. You want to buy 8 drinks and 9 hamburgers for you and your friends. How much do you expect to pay?PART B. Show your work or explain how you got your answer.

Answer 1

`\text{Total= \$43.5}`

Step by step explanation:

To solve this situation we can create a system of linear equations, with the given information for the customers:

Let x be the price for each hamburger

Let y be the price for each drink

`\begin{gathered} 2x+4y=13\text{ (1)} \\ 3x+7y=21\text{ (2)} \end{gathered}`

To solve for x and y. We can use the substitution method, which consists of isolating one variable in one of the equations and substitute it into the other.

Let's isolate y in (1):

`\begin{gathered} 4y=13-2x \\ y=(13)/(4)-(2)/(4)x \end{gathered}`

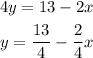
Now, substitute it into equation (2).

`3x+7((13)/(4)-(2)/(4)x)=21`

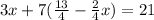
Solve for x:

`\begin{gathered} 3x+(91)/(4)-(7)/(2)x=21 \\ -(1)/(2)x+(91)/(4)=21 \\ -(1)/(2)x=21-(91)/(4) \\ -(1)/(2)x=-(7)/(4) \\ x=(7\cdot2)/(4) \\ x=(7)/(2)=\text{ \$3.5 } \end{gathered}`

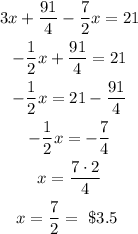
With the x-value, we can substitute it into the equation (1) to find the price for each drink:

`\begin{gathered} y=(13)/(4)-(2)/(4)(3.5) \\ y=(13)/(4)-(7)/(4) \\ y=(6)/(4)=\text{ \$1.5} \end{gathered}`

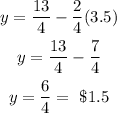
Therefore, the price for each hamburger is $3.5 and for each drink is $1.5.

Now, if we want to buy 8 drinks and 9 hamburgers:

`\begin{gathered} \text{Total}=(8\cdot1.5)+(9\cdot3.5) \\ \text{Total}=12+31.5 \\ \text{Total= \$43.5} \end{gathered}`