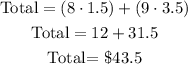Answer:

Step by step explanation:
To solve this situation we can create a system of linear equations, with the given information for the customers:
Let x be the price for each hamburger
Let y be the price for each drink
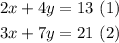
To solve for x and y. We can use the substitution method, which consists of isolating one variable in one of the equations and substitute it into the other.
Let's isolate y in (1):
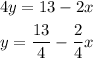
Now, substitute it into equation (2).
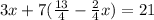
Solve for x:
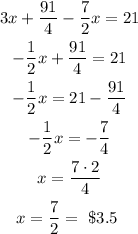
With the x-value, we can substitute it into the equation (1) to find the price for each drink:
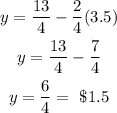
Therefore, the price for each hamburger is $3.5 and for each drink is $1.5.
Now, if we want to buy 8 drinks and 9 hamburgers: